|
相場の分析でよく利用している統計処理を紹介していきます。
[Ⅰ] 基本的な統計量
(1)データ数 n
分析の対象となるデータの数を表します。
(2)最大値 MAX
対象となるデータの最大値です。
(3)最小値 MIN
対象となるデータの最小値です。
(4)レンジ RANGE
対象となるデータにおける、最大値と最小値の差です。これをレンジと呼び”R”で表し,次式で求めます。
R = MAX - MIN
レンジは一般的にはあまり使用しない統計量ですが、相場を見る場合は1代足でどれだけの値幅があるか確認するときに使います。
(5)平均 : μ
一般にn個のデータ、X1,X2,X3,・・・Xn とある場合、その合計をnで割った値を示します。位置の代表値とも呼ばれおり、平均値をμ(ミュー)というギリシャ 文字で表しています。数式で表すと下記のようになります。
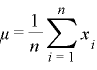
(6)標準偏差 : σ
標準偏差はデータのバラツキの尺度を表します。統計学においても最も重要な統計量の一つです。算出過程は以下のようになります。
Xi について個々のデータから平均値μを引いた値を偏差と呼びます。それぞれの偏差を2乗して合計した値を偏差平方和と呼び”S”で表します。偏差を2乗する意味は偏差をそのまま合計した場合プラスとマイナスで相殺されて0になるためバラツキの量が得られないからです。
そして偏差平方和Sをnで割ればバラツキを比較できる量を得ることができます。この値を分散と呼び”V”で表します。
そしてバラツキの尺度を元のデータと同じ単位に揃えるために分散Vの平方根をとります。こうして得られ値を標準偏差と呼び”σ”(シグマ)で表します。テクニカル指標ポリンジャーバンドのHiバンド、Lowバンドやブラックショールズ式のボラティリティの値としても使われています。
算出過程から標準偏差の数式は下記のようになります。
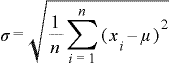
※標本から分散・標準偏差を求める場合、偏差平方和Sを自由度n-1で割ります。
(7)歪度 : β1
歪度はデータのカタヨリの尺度を表します。つまり与えれれた分布が左右対称であるかを調べるのに使います。歪度は次の式より求められます。
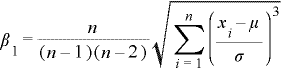
この値がマイナスになると分布が左側に偏り「左裾が重い」、また逆にプラスになると右側に偏り「右裾が重い」といわれます。サヤ取りを仕掛けるにあたって、逆ザヤ期になることが多い銘柄はこの値がマイナスになっている場合が多く、仕掛けずらい相場であるといえます。
(8)尖度 : β2
尖度はデータの尖りの尺度を表します。分布の頂上付近が鋭く尖っているか、または平坦に近く丸みかかっているかを調べるのに使います。尖度は次の式より求められます。
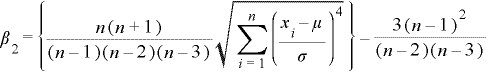
この値がマイナスになると標準に対して分布が平坦になり、また逆にプラスになると標準に対して分布が尖ります。サヤ取りを仕掛けるにあたって、この値が極端にマイナスをとっているとサヤが極端に離れて分布していることを意味し大きくサヤを取れる可能性もありますが、その分リスクも高くなるといえるでしょう。
※ここで紹介した統計量を求めるエクセルの関数を列記しておきます。
データ数 : =COUNT()
最大値 : =MAX()
最小値 : =MIN()
レンジ : =MAX()-MIN()
平均値 : =AVERAGE()
標準偏差 : =STDEVP()
歪度 : =SKEW()
尖度 : =KURT()
[Ⅱ] 確立分布について
ここではサヤデータにおける度数分布の統計処理のしかたと、変数”X”に対してその値が持つ確立を調べます。その時の変数”X”を確立変数と呼び、確立の集まりを確立分布と呼びます。代表的な4つの確立分布について紹介するとともにサヤ取りにおける各確率分布の利用例等についても簡単に書いておきます。
(1)度数分布
与えられたデータがある等間隔区間における密度の程度を調べます。この区間に入るデータの個数を数える統計処理を度数分布と呼びます。
度数分布は対象となるデータ全体の特徴を把握するのに使用します。例として東京白金6番限-3番限(2001年~2005年)のサヤデータを使います。今このサヤデータの全体が一定のサヤ値の間隔ごとにどれだけの数があるかを調べてみます。その結果が以下の表のようになりました。
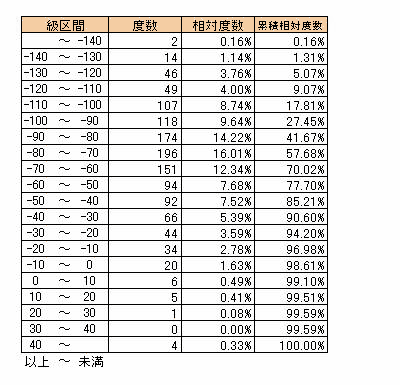 
サヤの値を-140、-130、・・・というような大きい単位にデータをまとめ級を作ります。それぞれの級区間に属するサヤデータの個数を級度数といいます。こうして得られる分布を組み分けによる度数分布といいます。上のように連続量で組み分けした度数分布は下のようなグラフにしてみることができます。
東京白金6-3番限サヤ ヒストグラム
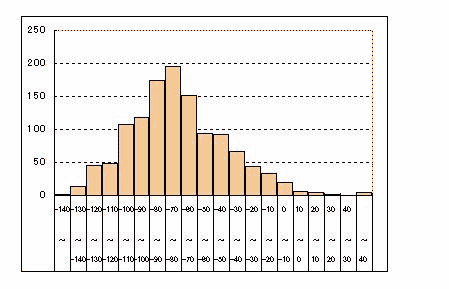
このように縦軸に度数、横軸に級区間値をとったグラフをヒストグラムと呼びます。
〔級区間の求め方〕
まず級の数ですが、データ数が十分に大きければ10~20くらいが適当かと思われます。そして対象となるデータのレンジを級の数で割れば級間隔を求めることができます。上の例ではレンジを20で割って四捨五入した値を級間隔としています。
級間隔 : 197÷20=9.85≒10
級限界値はデータの最大値と最小値を目安にして取ります。
上に得られたそれぞれの度数をデータ数で割った値で表した分布を相対度数分布と呼び、また相対度数を級の小さい方の値から順に加えていった値を累積相対度数と呼びます。累積相対度数を百分率(%)で表してグラフにした場合、下のようになります。
東京白金6-3番限サヤ 累積相対度数分布
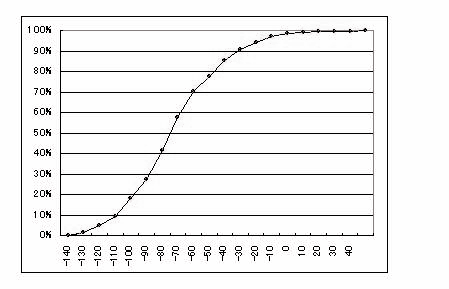
累積相対度数の50%の級の値がデータ平均値を示していることがわかります。また10%以下でサヤの値が約-110以下、90%以上でサヤの値が約-30以上であることがグラフから読み取ることができます。
例では東京白金6番限-3番限(2001~2005年)の度数分布を示しましたが、他の銘柄で同じような分析をしても必ずしも白金のようなきれいな分布の形をするとはいえません。これは白金が季節的要因でのサヤの変化がないためこのような6番限と3番限のサヤデータを扱うことができるからです。データ層ができるだけ同じ条件での分布を得ることを考えることが重要です。
(2)正規分布
確立密度関数が下の式で表される分布を正規分布と呼びます。
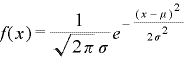
πは円周率3.14・・・、eはネイピア数2.73・・・
平均と分散はμとσ^2になります。この2つの数字がわかれば正規分布の形が定まり、N(μ、σ^2)と書きます。
正規分布を縦軸にf(x)、横軸にxをとると下のような釣鐘状のグラフになります。
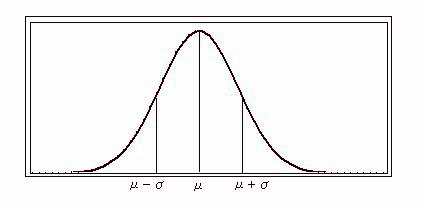
グラフを見てもわかるように正規分布には以下のような性質があります。
1.平均値μを中心に左右対称になっている。
2.確立密度関数は平均値μで一番高くなり、X軸を漸近線として両側に行くにつれ低くなる。
3.標準偏差σが大きくなればグラフが扁平に小さくなればグラフが狭く高くなる。またσは関数の変曲点になる。
4.f(x)とx軸で囲まれた面積は確立を意味し以下のような関係がある。関数で囲まれた部分の面積は積分で求めることができることから
(a)全体の面積〔-∞、∞〕は1になる。
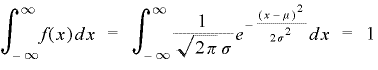
(b)μ-σとμ+σ間の面積は約0.68になる。
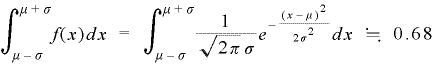
また
μ-2σとμ+2σ間の面積は約0.95、
μ-3σとμ+3σ間の面積は約0.99になる。
〔標準正規分布について〕
正規分布N(μ、σ^2)に従う変数Xに
z=(x-μ)/σ
という変換を施すと、zの平均は0、分散は1となる正規分布に従います。
z変換により変換された正規分布を標準正規分布と呼び、N(0,1)で表します。標準正規分布のzがわかれば、わざわざ上にあるような積分の計算をしなくとも一般に公開されている統計値表より正規分布の確立を求めることができます。
次に前の度数分布で扱った東京白金のデータを標本として正規分布で近似した場合どのような結果が得られるか見ていきたいと思います。
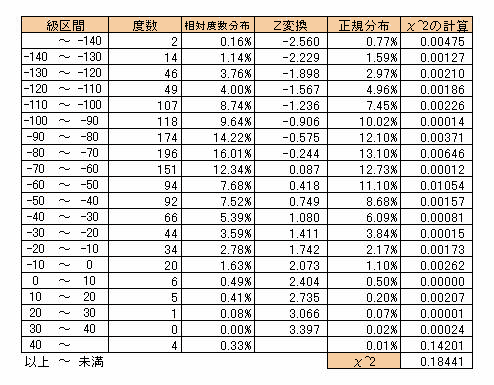
まずそれぞれの級の値にz変換を施し標準正規分布から確立を算出します。
これで得られた正規分布と相対度数分布の関係をグラフにしてみます。
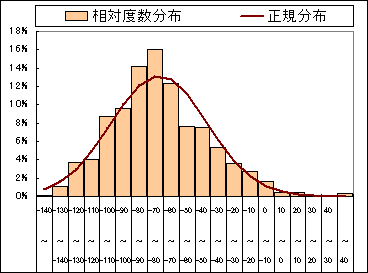
グラフをみると相対度数分布と正規分布がほほ近似しているのがわかります。
〔適合度の検定〕
相対度数分布と正規分布との差が大きいとき、正規分布にあてはまるという仮説を棄却することにするという検定を行う場合、相対度数分布と正規分布との差を測るものさしとして次式で与えられる量χ^2(カイ2乗)が用いられます。
χ^2=Σ(相対度数分布-正規分布)^2/(正規分布)
χ^2がχ(k-3、0.05)より大きいとき仮説が捨てられる。
自由度は級の数kから3引いた数をとります。(正規分布の平均と標準偏差を推定したため)
χ^2=0.18<χ^2(17,0.05)=27.6 *カイ2乗表より
となり仮説は棄却され有意水準95%で正規分布に従う。
※適合度の検定は確立分布にデータ数nをかけることにより期待度数を算出し、期待度数と実測度数の検定を行うのが一般的ですが、相場において扱う時系列データの実測値は分布の両側にデータの偏りが現れることが多いので仮説が捨てられる場合がほとんどです。そこで相対度数分布と正規分布が上のグラフのように視覚的に近似しているのを確認した上で、上記の検定をすればよいのではと思います。
以上を踏まえた上で、実際にどのような相場の張り方をすればよいか、東京白金のサヤを例に挙げてみます。正規分布の右側を上限、左側を下限として各々の片側の確立に対応するサヤ値を求めて下のような表にまとめてみます。
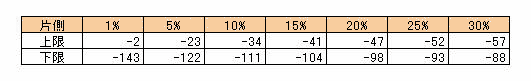
例えばサヤ値が上限の10%以下(-34以上)になった場合は逆ザヤ取りを仕掛け、下限の10%以下(-11以下)になった場合は順ザヤ取りを仕掛けるなどの手法が有利になりそうです。
※正規分布を求めるエクセル関数式
=NORMDIST(x,平均,標準偏差,関数形式)
また標準正規分布の累積確立(-∞~z)は次の関数より求められます。
=NORMSDIST(STANDARDIZE(x,平均,標準偏差))
(3)二項分布
1回のトレードにおいて勝率70%のシステム売買があると仮定します。このトレードを4回(n=4)繰り返した場合、起こりえる確率がどのようになるか下表でみてみます。
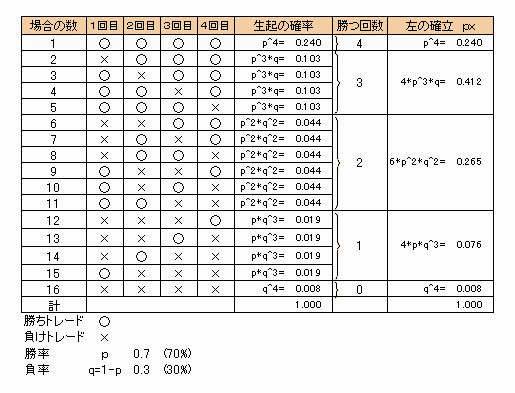
表みてもわかるように起こりえる場合は16通りありますが、勝つ回数という事象にだけ注目すれば、0,1,2,3,4の5通りあります。例えば2回だけ勝つ場合は、何回目と何回目で勝つかという組み合わせの数より6通りあり、その確立は6*p^2*q^2=0.265になります。勝つ回数0,1,2,3,4ごとに確立pxを与える確立分布になることがわかります。
例のように勝つか負けるかというような事象が2通りしか起こらない分布を二項分布と呼び、その確立pxを表す一般式は以下のようになります。
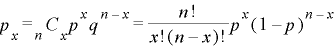
n=10のときp=0.1,p=0.3,p=0.5に変えた場合の2項分布のグラフを以下に示します。
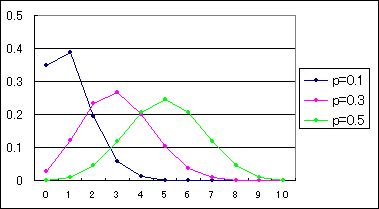
p=0.1のときはx=0やx=1のときに大きな山があり、p=0.3のときはx=3のとき山になり、p=0.5のときはx=5のとき山になりさらに左右対称になっていることがわかります。
投資においてはリスク管理の概念の一つとして使われます。
※二項分布を求めるエクセル関数式
=BINOMDIST(成功数,試行回数,成功率,関数形式)
(4)ポアソン分布
二項分布においてμを固定したままで、nを十分に大きくし、それに伴いpを十分に小さくしたときの極限分布を求めると。以下のような式が導き出されます。
(数学的な算出過程は省略します)
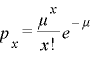
上の確立を取る分布をポアソン分布と呼びます。
式をみてもわかるようにポアソン分布の確立pxは平均μの値のみで定まることがわかります。下に平均μの値をいろいろと変えた場合にどのようなグラフになるか描いてみます。
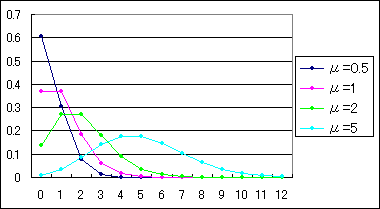
その確立pxはμが小さい場合はx=0のとき最大となり、μが大きくなるにつれポアソン分布が山形に変化していきます。μが5以上になると、分布はほぼ左右対象になり正規分布に近似していきます。
このポアソン分布は何を意味するのかというと、ある一定の長さの期間、一定の大きさの空間において、ごくまれに起こる事象の数を表す確立分布を取ります。
例えばシステム売買において1週間に仕掛けの数が平均何回あるかとか分割売買をする場合はその頻度は平均何回かとかを確立的に算出して、どれだけの資金を用意すればよいかなど目安を計ることができそうです。1週間の平均仕掛けか回数が1回の場合は上に示したグラフのμ=1の確立を取ります。
※ポアソン分布を求めるエクセル関数式
=POISSON(イベント数,平均,関数形式)
(5)指数分布
指数分布はある条件の下で決められた事象が起きるまでの時間を表す、つまり到来時間がこの分布に従います。
指数分布の確立密度関数は以下のように表されます。(Xは負の値をとらない)
ここでのλは平均到来時間は1/λの逆数を意味します。
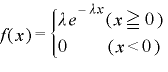
式をみてもわかるようにポアソン分布の確立f(x)はλの値のみで定まることがわかります。下にλの値をいろいろと変えた場合、次のようにグラフが変化します。
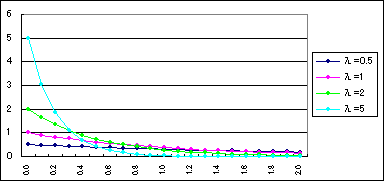
システム売買において次の仕掛けが何日以内に○%の確立で発生するとかなどを計算するのに使ったりします。
※指数分布を求めるエクセル関数式
=EXPONDIST(x,λ,関数形式)
以上4つの確率分布について説明しましたが、これらの分布は2つのタイプに分かれます、2項分布やポアソン分布は確率変数”X=1,2,3、・・・”のようなある一点に対して確立が存在する離散型確率分布と呼ばれ、対し正規分布や指数分布はある一点に対しての確立は存在しなく”0≦X≦3”のようなある区間に対して確立が計れる連続型確率分布と呼ばれます。連続型の確立分布の数式は至る所で積分可能な確立密度関数を持ちます。
[Ⅱ] モーメントについて
確率分布には期待値や分散といった統計的な数量が存在しますので、これらの統計量についても少し触れておきましょう。まず期待値ですが、これは確立変数Xは平均的にどれくらいの数量を表すのかというものです。
わかりやすい例で1枚300円の宝くじがあって、それを日本中の宝くじを買い占めたとします。この宝くじの当たった金額をすべて集計して、購入した日本中の宝くじの枚数で割り算した値が140円だったとします。これがこの宝くじの期待値になります。また1等から末等までの当選金額が確率変数となり、各々の当選本数を全発行枚数で割った値が確立となる確立分布を意味します。
一方、分散とは確立変数の期待値からどれくらいバラツキがあるかを示す尺度を表します。さらに確率変数の分散から平方根を取った値を確立変数の標準偏差といいます。
ここで注意しなければならないのは、確率分布の期待値や分散は統計データの平均や分散または標準偏差とは全く別の意味を表し、区別して考えなければなりません。
一般的には確率分布の期待値E(X)と分散V(X)は以下の公式と法則から求められます。
■期待値の公式
| (離散型) |
(連続型) |
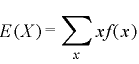 |
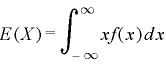 |
■分散の公式
| (離散型) |
(連続型) |
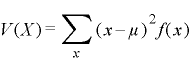 |
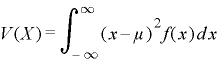 |
分散V(X)は右辺のを変形して以下のように期待値を求めれば簡便化できます。
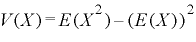
E(X)とV(X)は確率過程の分野やポートフォリオの構築で頻繁に使われますのでしっかりと覚えておく必要があります。
上に紹介した4つの確率分布の期待値と分散はE(X)とV(X)の公式から以下のように求められます。尚、導出過程の証明や計算まではここでは説明しませんが、結果だけを紹介しておきます。
(1)二項分布の期待値と分散
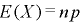 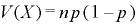
(2)ポアソン分布の期待値と分散
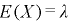 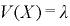
(3)指数分布の期待値と分散
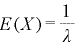 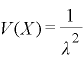
(4)正規分布の期待値と分散
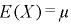 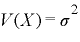
確率分布を調べるのに1次モーメントである期待値や2次のモーメントである分散はよく使われますが、一般的には3次モーメントである歪度や4次のモーメントえある尖度を表すモーメントも必要になります。このようにすべての次数のモーメントを求めれば一つの確率分布が決定されます。5次以降のモーメントついては何を表しているのかはわかっていませんが、何かを表しているらしいです。
すべての次数を表すモーメントは次のモーメント母関数で定義されています。
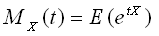
| (離散型) |
(連続型) |
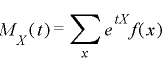 |
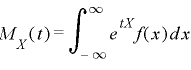 |
連続型は実質関数のラプラス変換であり、前回のフーリエ変換に次いで重要な積分変換です。
モーメントを求めるにはモーメントの階数だけ上式を微分してt=0と置くと、高次の項が消えて、求めるモーメントだけ残ります。(ただしすべての関数が微分できるとは限りません)
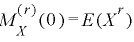
証明は下記のようにモーメント母関数の右辺をテイラー展開することにより得られます。
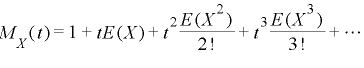
ここで紹介した4つの確率分布のモーメント母関数は次のようになります。
(1)二項分布のモーメント母関数
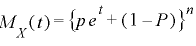
(2)ポアソン分布のモーメント母関数
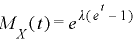
(3)指数分布のモーメント母関数
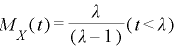
(4)正規分布のモーメント母関数
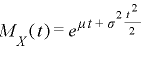
|

