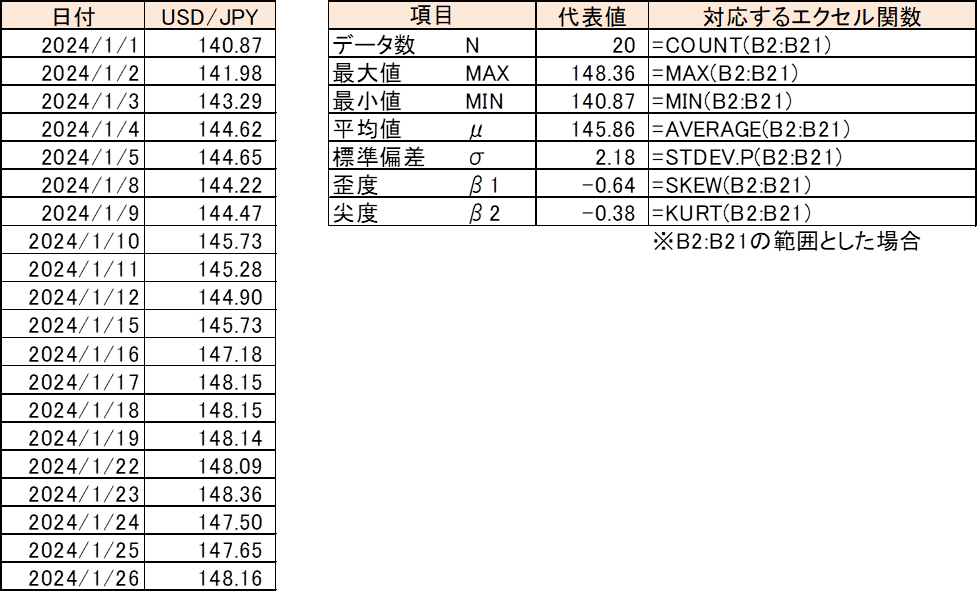
データを分析に使用する代表値について解説をしていきます
下記の他にも様々な統計量はありますが、ここでは実際の相場の分析あたって実用的なものをいくつか解説します。
① データ数:N
分析の対象となるデータの数を表します。日足終値の推移など時系列データをメインに取り扱います。データ数が多いほど精度の高い分析が期待できます。
② 最大値:MAX
分析の対象となるデータの最大値になります。相場では任意の期間における最高値を表します。
③ 最小値:MIN
分析の対象となるデータの最小値になります。相場では任意の期間における最安値を表します。
④ 平均値:μ(ミュー)
平均値はN個のデータの合計をNで割った値になります。インジケータの単純移動平均線などを算出します。
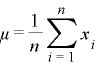
⑤ 標準偏差:σ(シグマ)
標準偏差はデータのバラツキの尺度を表します。個々のデータXi から平均値μを引いた値を偏差と呼びます。それぞれの偏差を2乗して合計した値を偏差平方和と呼びます。偏差平方和をデータ数Nで割ればバラツキを計る量を得ることができます。この値を分散と呼びます。そしてバラツキの尺度を元のデータと同じ単位に揃えるために分散の平方根をとります。こうして得られた値を標準偏差と呼び”σ”(シグマ)で表します。インジケータのポリンジャーバンドで使用されるバンドの幅(σ)はこのように求められています。
算出過程から標準偏差を求める数式は下記のようになります。
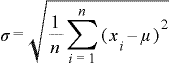
⑥ 歪度(わいど):β1
歪度はデータの歪みの尺度を表します。データのバラツキが左右対称であるかを調べるのに使います。歪度は次の式より求められます。
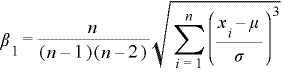
この値がマイナスになると分布が左側に偏り「左裾が重い」、また逆にプラスになると右側に偏り「右裾が重い」ます。正規分布では0になります。
⑦ 尖度(せんど):β2
尖度はデータの尖りの尺度を表します。分布の頂上付近が鋭く尖っているか、または平坦に近く丸みかかっているかを調べるのに使います。尖度は次の式より求められます。
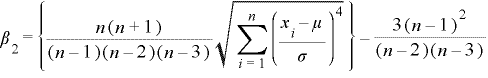
この値がマイナスになると標準に対して分布が平坦になり、また逆にプラスになると標準に対して分布が尖ります。正規分布では0になります。
歪度と尖度は相場の値動き(値幅)の分布を分析するのに使用します。相場の値動きというものは平均的にこのくらいというのがあっても均等な分布になっていることは稀です。レンジ相場の場合は価格の値動きは小さいですが、トレンドが発生したときには大きく動き出します。これら全体としての値動きとしてみた場合、歪みや尖りがある分布になることは想像がつくかと思います。これらを数値的な尺度でとらえるようにすることで、利確や損切りの基準を設定していきます。
また歪度と尖度に至っては数式を覚える必要はありません。このサイトではできるだけ計算の仕方を残すようにしたいので計算式を掲載するようにしています。
最後にここで紹介した統計量の計算例を掲載しておきます