相関について

サヤ取りを実践するにあたって、２つの銘柄に相関関係があることが絶対条件です。相関とはどういうものかとその扱い方について解説していきます。

相関関係とは２つのものが関わりあい、一方が変動すれば、それに応じてもう一方も変動するいうもので、例えばほWTI原油の価格が上がれば、北海ブレント原油の価格もそれに応じて上がるというような関係性のものです。このように２つの銘柄が同じ方向に動く関係を順相関があるといいます。また一方の動きに対して逆の方向に動く関係を逆相関があるといいます。

この相関関係の強弱を示す指標として統計学において相関係数というもがあり、－１から１までの値をとります。この相関係数が”１”に近づけば順相関の関係があり、”－１”に近づけば逆相関の関係があり、また相関係数が”０”に近ければ無相関であることと解釈されます。

ＸとＹの相関係数”r”を求める式は以下になります。

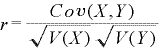
上式のＶ（Ｘ）、Ｖ（Ｙ）はＸ，Ｙそれぞれの分散を表し、Ｃｏｖ（Ｘ，Ｙ）はＸとＹの共分散を表します。

共分散とはＸとＹがそれぞれの平均との偏差の積に関連してバラツク尺度を表しています。

ここでのＶ（Ｘ）、Ｖ（Ｙ）、Ｃｏｖ（Ｘ，Ｙ）の数式の定義は以下になります。

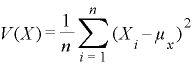
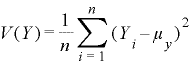
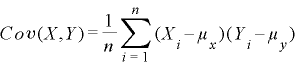
Ｃｏｖ（Ｘ，Ｙ）の値がプラスならＸとＹの変動が同傾向、マイナスなら逆傾向の関係があります。

また分散Ｖ（Ｘ）と共分散Ｃｏｖ（Ｘ，Ｙ）にはいろいろな重要な性質があります。特に下記の２つの式は重要ですのでその性質を覚えておく必要があります。

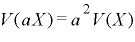
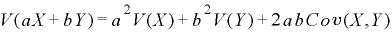
（１）式はある銘柄Ｘを１ロット（a=1）持つときの分散Ｖ（Ｘ）に対して２ロット（a=2）持つときの分散Ｖ（２Ｘ）は４Ｖ（Ｘ）となりその変動リスクは４倍になるということを意味します。Ｘの係数はその分散をとった場合、単純にa倍になるのではなくて、２乗に比例することになります。

（２）式はある銘柄ＸとＹのポジションを持ったとき、その分散Ｖ（Ｘ）+Ｖ（Ｙ）は個々の分散値V（Ｘ）、Ｖ（Ｙ）を単純に足した値にはならず、それに共分散Ｃｏｖ（Ｘ，Ｙ）を加えて等式が成り立ちます。

サヤ取りを実践する場合、相関係数が高い低いで仕掛ける銘柄の組み合わせを考えるのも大切ですが、その組み合わせにおける分散の加法性をみることも大事なことです。

最後に相関のある組み合わせを選択した銘柄の実践例を１つ紹介します。（例として説明のしやすい組み合わせを意図的に選んでおり、推奨する組み合わせではありません）

相関関係の高い組み合わせとしてＥＵＲ/ＵＳＤとＺＡＲ/ＪＰＹの通貨ペアを例に説明します。この組み合わせの相関係数は”-0.835”とまずまず高い逆相関の関係があるといえます。この場合双方の通貨ペアが下の表のように反対の方向に動く傾向があるため、ＥＵＲ/ＵＳＤロングとＺＡＲ/ＪＰＹロングの組み合わせもしくはＥＵＲ/ＵＳＤショートとＺＡＲ/ＪＰＹショートの組み合わせが双方の変動リスクを相殺するのに有効です。仮に相関係数がプラスの場合は片方をロングもう片方をショートにすることは言うまでもありません。

次にこの組み合わせの組込み比率を決めていきます。ここで分散と共分散の公式が必要になってきます。組み合わせの分散を最小にするには、V（aX+bY)が最小になる”a”と”b”の値を求めればよいということになります。求め方は最小２乗法といわれる方法で、上の（２）式を”a”と”b”で偏微分して”=0″と置くやり方で解きます。また数学的証明は省きますが”V(aX+bY)”はV(X)*V(Y)≧Cov(X,Y)^2の関係から必ず０以上の値をとります。

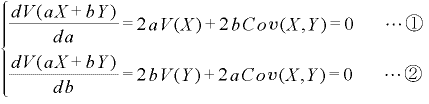
①式、②式から”a”と”b”について整理すると以下のような関係式が出来上がります。また”a”と”b”を比率で表すため”a+b=1”という条件を付け加えます。

③と④の連立方程式を”a”と”b”について解くと

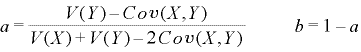
となり、この”a”と”b”がV（aX+bY)が最小となりうるV(X)とV(Y)の組み込む比率を意味します。

次に上の例での組み込み比率を計算してみましょう。

変数はＸ＝ＥＵＲ/ＵＳＤ、Ｙ＝ＺＡＲ/ＪＰＹに割り当てます。通貨ペアの分散・共分散は

　　　V(X)=68.867　　V(Y)=2.8　　 Cov(X,Y)=-11.602

になってますので、組み込み比率は

　　　a=0.152　　b=0.848

となり、求めるべきV(aX+bY)の最小値は

　　　V(aX+bY)=V(0.152X+0.848Y)=(0.152)^2 * 68.867 + (0.848)^2 * 2.8 + 2 * 0.152 * 0.848 * (-11.602) = 0.614　

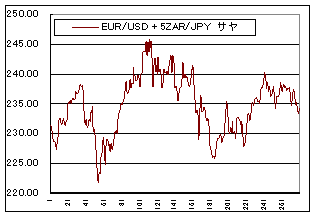
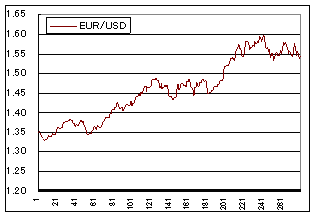
と求まります。これは”Ｘ”に対して”Ｙ”が”a:b”の比率で組み込めば、最もボラティリティが抑えられるということになります。比率はＥＵＲ/ＵＳＤを１ロットに対してＺＡＲ/ＪＰＹを５ロットにすればよさそうです。この比率で組み入れた”ＥＵＲ/ＵＳＤ+５*ＺＡＲ/ＪＰＹ”のサヤグラフを個々通貨ペアのボラティリティと比較しながら見てみましょう。ずいぶんボラティリティが抑えられらていることが見てわかります。

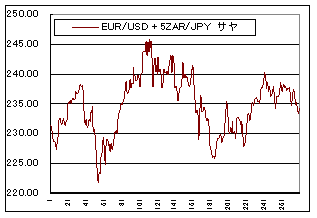
　　　　Ｖ（ＥＵＲ/ＵＳＤ）＝68.867

　　　　Ｖ（５*ＺＡＲ/ＪＰＹ）＝70.001

　　　　Ｖ（ＥＵＲ/ＵＳＤ+５*ＺＡＲ/ＪＰＹ）＝22.859

相関に関しての解説をしてきましたが、注意するところは選んだ銘柄がファンダメンタル的要因などで値動きが極端に強くなったり、弱くなったりすることは度々起こるものです。相関関係が無くなってしまうことがあります。そのときはポジションは速やかに手を引くこということが鉄則です。定期的に相関関係チェックすることは大事です。