|
廳夞婣暘愅傪娙扨偵尵偆偲偄傠偄傠側尨場偲偦偺寢壥傪寢傃偮偗傞懡曄検夝愅偵側傝傑偡丅
椺偊偽寢壥偲偟偰柧擔偺抣摦偒偼梲慄偱堷偗傞偐傕偟偔偼堿慄偱堷偗傞偐偼丄尨場偲偟偰偺條乆側僥僋僯僇儖巜昗偲偺場壥娭學傪暘愅偟偰傒傞偙偲側偳偑嫇偘傜傟傑偡丅偙偺尨場偑攧攦僔僗僥儉偵偍偗傞儘僕僢僋偲偟偰丄柧擔偺抣摦偒偵偳偆斏塰偝傟傞偐側偳傪専徹偡傟偽丄桳岠側僔僗僥儉儘僕僢僋偑尒偮偐傞偐傕偟傟傑偣傫丅
偙偙偱偼娙扨側巇妡偗僒僀儞偲偺場壥娭學傪挷傋傞廳夞婣暘愅偺椺傪宖嵹偟偰偍偒傑偡丅
廳夞婣暘愅偼偄偔偮偐偺尨場傪倃1丄倃2丄倃3丒丒丒偲偟偰偦偺寢壥倄偲偟偨応崌師偺傛偆側娭學幃傪嶌傝傑偡丅
丂丂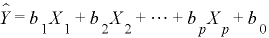
偙偺幃傪廳夞婣幃偲屇傃丄倃1丄倃2丄倃3丒丒丒傪愢柧曄悢丄倄^傪栚揑曄悢側偳偲屇偽傟丄奺愢柧曄悢偺學悢b1丄b2丄b3丒丒丒偼曃夞婣學悢偲屇偽傟傑偡丅b0偼掕悢崁偵側傝傑偡丅
幚嵺偺暘愅偺棳傟偼埲壓偺傛偆偵側傝傑偡丅
嘆廳夞婣暘愅傪偡傞堄枴偑偁傞偺偐奺愢柧曄悢偲栚揑曄悢偺嶶晍恾傪昤偄偰傒傞丅
嘇廳夞婣幃傪媮傔傞丅
嘊廳夞婣幃偺惛搙傪妋擣偡傞丅
嘋廳夞婣幃偲曃夞婣學悢偺専掕傪峴偆丅
嘍曣夞婣幃傪悇掕丄梊應偡傞丅
偱偼嬶懱揑側椺偱廳夞婣暘愅傪幚峴偟偰傒傑偟傚偆丅
暘愅偵巊梡偡傞僨乕僞偲偟偰俤倀俼/俰俹倄亊俀偲俠俫俥/俰俹倄亊俁偺廡娫僒儎僨乕僞丄俀侽侽侽擭侾寧偐傜俀侽侽俋擭侾俀寧暘傪巊梡偟傑偡丅
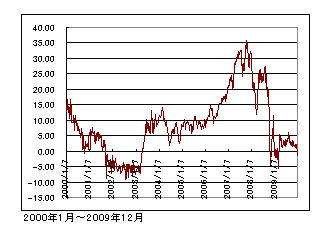
丂丂俤倀俼/俰俹倄亊俀-俠俫俥/俰俹倄亊俁丂僒儎僌儔僼
偦傟偱偼忋偺棳傟偺偲偍傝弴斣偵暘愅傪峴偄傑偡丅
嘆廳夞婣暘愅傪偡傞堄枴偑偁傞偺偐奺愢柧曄悢偲栚揑曄悢偺嶶晍恾傪昤偄偰傒傞丅
傑偢巒傔偵曄悢偺愝掕傪峴偄傑偡丅偙偙偱偼師偺傛偆偵栚揑曄悢偲愢柧曄悢偺掕傔傑偡丅
廡娫僒儎曄摦抣丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂佀丂栚揑曄悢乭倄乭
侾偮慜偺廡娫僒儎曄摦抣丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂佀丂愢柧曄悢乭倃1乭丄
僒儎偺昗弨曃嵎乮侾俆廡乯偵榗搙乮侾俆廡乯傪妡偗偨抣乮仸乯丂佀丂愢柧曄悢乭倃2乭偲愝掕偟傑偡丅
仸側偤偙偺傛偆側張抲傪偡傞偺偐偲偄偆偲昗弨曃嵎偼昁偢惓偺抣傪庢傝傑偡偺偱僾儔僗儅僀僫僗椉曽傪庢傞僒儎偺曄摦抣倄偲夞婣暘愅傪峴偆応崌丄侾師幃偱摉偰偼傔傞偙偲偑弌棃側偄偨傔偱偡丅傑偨僶儔僣僉偵傂偢傒偺広搙傪崌傢偣傞偙偲偵傛偭偰僒儎偺曄摦偑戝偒偔偐偮僒儎偺暘晍偑惓婯暘晍偵側偭偰側偄忬懺傪恾傞広搙偲偟偰巊偊傞偺偱偼側偄偐偲偄偆巚榝傕偁傝傑偡丅
愢柧曄悢倃1偲倃2偲栚揑曄悢倄偵偮偄偰偺嶶晍恾偼偦傟偧傟埲壓偺傛偆偵側傝傑偡丅
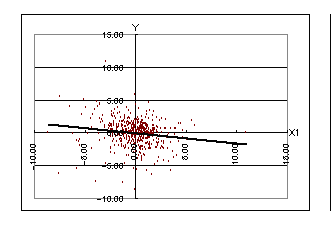 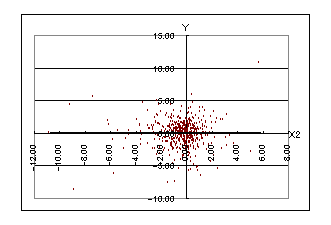
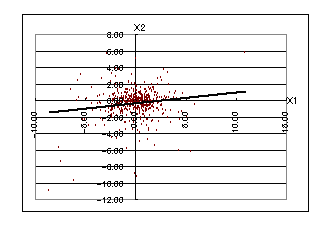
嶶晍恾傪尒偰傕傢偐傝傑偡偑丄倃1偲倄偺娭學偵偼庒姳晧偺憡娭偁傝偦偆偱偡丅偙傟偼慜偺廡僒儎偑奼戝偵摦偄偨応崌偼偦偺梻廡偼弅彫偵丄媡偵慜偺廡僒儎偑弅彫偵摦偄偨応崌偼偦偺梻廡偼奼戝偵摦偔孹岦偑偁傞偙偲傪堄枴偟偰偄傑偡丅
師偵倃2偲倄偺娭學傪尒偰傒傑偡偙傟偵偼慡偔憡娭偑側偝偦偆偱偡偑丄倃侾偲倃俀偺娭學偵偼彮偟惓偺憡娭偑偁傞偙偲偑婥偵偐偐傝傑偡丅
埲忋偐傜倃1丄倃2丄倄偵偼側傫傜偐偺娭學偑偁傞偲巚傢傟傑偡偱丄廳夞婣暘愅傪偟偰傒傞壙抣偑偁傞偺偱偼偲敾抐偟傑偡丅
嘇廳夞婣幃傪媮傔傞丅
幚應抣倄偲梊應抣倄丱偺嵎偺暯曽榓傪巆嵎暯曽榓偲屇傃俽e偱昞偟傑偡丅
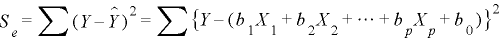
廳夞婣幃偼偙偺巆嵎暯曽榓俽e傪嵟彫偵偡傞婎弨偵傛偭偰媮傔傜傟傑偡丅
偡側傢偪忋偺幃偑嵟彫偵側傞傛偆側倐0乣倐倫傑偱偺夞婣學悢傪媮傔傟偽傛偄傢偗偱偡偐傜丄奺夞婣學悢傪曃旝暘偟偰侽偲抲偔嵟彫俀忔朄偱媮傔傟偽傛偄偙偲偑傢偐傝傑偡丅
丂丂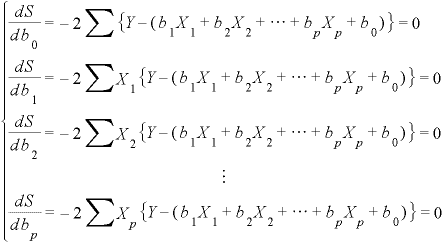
忋偺楢棫曽掱幃傪夝偄偰倐0乣倐倫傑偱偺夞婣學悢傪媮傔傟偽廳夞婣幃偑掕傑傝傑偡丅
幚嵺偵杮椺偱媮傔偨廳夞婣幃偼埲壓偺傛偆偵側傝傑偟偨丅
丂丂倄^ = -0.159X1 + 0.027X2 - 0.017
嘊廳夞婣幃偺惛搙傪妋擣偡傞丅
媮傔偨廳夞婣幃
丂丂倄^ = -0.159X1 + 0.027X2 - 0.017
偼偳偺掱搙幚嵺偺僨乕僞偵摉偰偼傑偭偰偄傞偐丄偦偺摉偰偼傑傝偺椙偝傪昞偡偺偵寛掕學悢偲偄偆広搙偑巊傢傟傑偡丅
寛掕學悢傪媮傔傞偁偨偭偰埲壓偺摑寁検傪媮傔傑偡丅
幚應抣倄偺曃嵎暯曽榓丂丂俽t
梊應抣倄丱偺曃嵎暯曽榓丂丂俽r
幚應抣倄偲梊應抣倄丱偺嵎偺暯曽榓偡側傢偪巆嵎暯曽榓丂丂俽e
偝傜偵偙偺俁偮暯曽榓偵埲壓偺傛偆側娭學幃偑惉棫偟偰偄傑偡丅
丂丂俽t = 俽r + 俽e
偙偺偙偲偐傜摉偰偼傑傝昞偡傪広搙偼幚應抣倄偺曃嵎暯曽榓俽t偺忣曬検偺拞偵梊應抣倄丱偺曃嵎暯曽榓俽r偺忣曬検偑偳傟偩偗娷傑傟偰偄傞偐傒傟偽傛偄偙偲偑傢偐傝傑偡丅偙傟傪斾棪偱昞偟偨広搙偑寛掕學悢乮俼丱2乯偵側傝傑偡丅
丂丂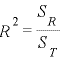
傑偨寛掕學悢乭俼丱2乭偼幚應抣倄偲梊應抣倄丱偺憡娭學悢偺俀忔偲摍偟偔側傝傑偡丅偦傟備偊偵偙偺乭俼乭偼廳憡娭學悢偲屇偽傟偰偄傑偡丅偳偪傜傕摉偰偼傑傝偺椙偝傪昞偡広搙偲偟偰巊傢傟偰偄傑偡丅
杮椺偱媮傔偨寛掕學悢媦傃廳憡娭學悢偼埲壓偺傛偆偵側傝傑偟偨丅
丂丂寛掕學悢丂俼丱2 = 0.025 丄廳憡娭學悢丂俼 = 0.157丂
堦斒揑偵侾偮偺栚埨偲偟偰寛掕學悢偼0.5埲忋丄廳憡娭學悢偼0.7埲忋偁傟偽摉偰偼傑傝偑傛偄偲偝傟偰傑偡偑丄崱夞偺寢壥傪傒傟偽慡慠抣偑彫偝偔梊應幃偑摉偰偼傑偭偰側偄偲夝庍偱偒傑偡丅偦傕偦傕攧攦儘僕僢僋偵偦傟傎偳惛搙偺崅偄梊應幃偑懚嵼偡傞偼偢偑側偄偺偑摉偨傝慜偱偡丅巹傕偙偺傛偆側暘愅傪悢懡偔傗偭偰偒傑偟偨偑廳憡娭學悢偑0.2傪挻偊傞偙偲偼婬偱偡丅偱偡偑幚嵺偺僔僗僥儉攧攦偵偍偄偰庒姳偱傕憡娭偑偁傟偽丄偦傟偑嫮椡側儘僕僢僋偑懚嵼偡傞偙偲傪愢柧偟偰偄傞応崌傕偁傝傑偡丅屄恖揑偵偼廳憡娭學悢0.2晅嬤乮媡憡娭偺応崌偼-0.2乯傪栚埨偲偟偰偍傝傑偡丅
嘋廳夞婣幃偲曃夞婣學悢偺専掕傪峴偆丅
媮傔偨廳夞婣幃偑梊應偵栶棫偮偐偳偆偐挷傋傞偨傔偵埲壓偺傛偆側専掕傪峴偄傑偡丅
専掕偵偼曣廤抍忋偺儌僨儖偲偟偰師偺傛偆側廳夞婣儌僨儖傪愝掕偟傑偡丅
丂丂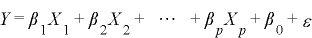 丂丂丂 乭兠乭偼岆嵎傪昞偟傑偡 丂丂丂 乭兠乭偼岆嵎傪昞偟傑偡
偙偺儌僨儖偵懳偟偰壖愢傪棫偰専掕傪峴偄傑偡丅
仭廳夞婣幃偺専掕
丂壖愢丂俫0 丗 兝1亖兝2亖侽
偙傟偼夞婣學悢兝1偲兝2偑侽偱偁傟偽梊應偡傞偙偲偑偱偒側偄偲偄偆壖愢偵側傝傑偡丅
偙偺専掕偵偼師偺傛偆側暘嶶暘愅昞傪巊偄傑偡丅杮椺偱寁嶼偟偨暘嶶暘愅昞傪宖嵹偟傑偡丅
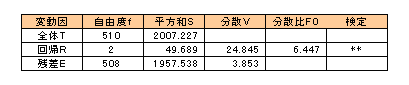
偙偺昞偼慡僨乕僞悢乭n乭偺曄摦偺慡懱俿偑夞婣俼偺晹暘偲巆嵎俤偺晹暘偵暘偗傜傟傞曄摦場傪暘愅偟傑偡丅
帺桼搙倖偼奺曄摦場偐傜撈棫偵慖傋傞僨乕僞悢偱師偺傛偆偵寁嶼偝傟傑偡丅
倖T = n-1
fR = p 乮p偼愢柧曄悢偺悢乯
fE = n-p-1
暯曽榓俽偼偦傟偧傟埲壓偺抣傪偲傝傑偡
丂俽t丂幚應抣倄偺曃嵎暯曽榓丂丂
丂俽r丂梊應抣倄丱偺曃嵎暯曽榓丂丂
丂俽e丂巆嵎暯曽榓丂丂
暘嶶倁偼偦傟偧傟暯曽榓俽傪帺桼搙倖偱妱偭偨抣偵側傝傑偡丅
暘嶶斾俥0偼夞婣偺暘嶶倁俼傪巆嵎偺暘嶶倁俤偱妱偭偨抣偵側傝傑偡丅
俀偮偺暘嶶斾偼俥暘晍傪偡傞偙偲偵側傝傑偡偺偱丄専掕偱偼偙偺暘嶶斾俥0偺抣傪巊梡偟傑偡丅壖愢偑惓偟偔側偗傟偽倁俼偑倁俤傛傝傕彫偝偔側傞偙偲偼側偄偺偱丄偙傟偺桳堄悈弨傪専掕偡傟偽傛偄偙偲偵側傝傑偡丅
俥抣偼帺桼搙fR丄fE 丄偲桳堄悈弨兛偱寛掕偟傑偡偺偱
俥0亜俥乮fR丄fE 丄兛乯偱偁傟偽兛偺桳堄悈弨偱壖愢偐婞媝偝傟傞偙偲偵側傝傑偡丅
忋偺昞偺専掕偱偼桳堄悈弨兛偑俆亾偱婞媝偝傟傟偽乽*乿偱儅乕僋偟偰丄桳堄悈弨兛偑侾亾偱婞媝偝傟傟偽乽**乿偱儅乕僋偡傞傛偆偵偟偰偍傝傑偡丅
杮椺偱偼桳堄悈弨侾亾偱壖愢偑婞媝偝傟偰傑偡偺偱丄媮傔偨廳夞婣幃偼梊應偵栶棫偮偲敾抐偱偒傑偡丅
仭夞婣學悢偺専掕
屄乆偺夞婣學悢偺専掕偱偼埲壓偺傛偆側壖愢傪棫偰傑偡丅
丂壖愢丂俫0 丗 兝1亖侽丂乮慜廡偺僒儎曄摦偼梻廡偺僒儎偺曄摦偵塭嬁偟側偄乯
丂壖愢丂俫0 丗 兝2亖侽丂乮僒儎偺昗弨曃嵎*榗搙偼梻廡偺僒儎偺曄摦偵塭嬁偟側偄乯
師偺摑寁検傪傕偲傔偰倲暘晍偵傛傞専掕傪峴偄傑偡丅
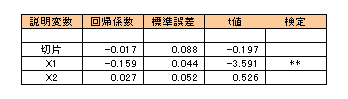
昗弨岆嵎偲偼悇掕抣偺昗弨曃嵎偺偙偲偱埲壓偺傛偆側幃偱媮傑傝傑偡丅
愢柧曄悢偺昗弨岆嵎
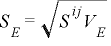
掕悢崁乮愗曅乯偺昗弨岆嵎
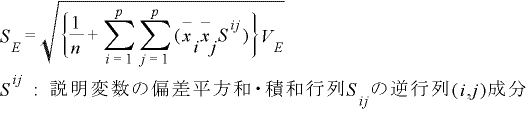
夞婣學悢傪昗弨岆嵎偱妱偭偰倲抣傪媮傔桳堄惈偺専掕傪峴偄傑偡丅
倲0亜倲乮n-p-1丄兛乯偱偁傟偽兛偺桳堄悈弨偱壖愢偐婞媝偝傟傞偙偲偵側傝傑偡丅
夞婣學悢倐侾偼桳堄悈弨侾亾偱壖愢偑婞媝偝傟偰傑偡偺偱丄廳夞婣幃偼娷傑偣傞偙偲偑傛偄偲敾抐偡傞偙偲偑偱偒傑偡丅
夞婣學悢倐俀偼桳堄偱偼偁傝傑偣傫偺偱丄廳夞婣幃偼娷傑偣側偔偰傕塭嬁偼側偄偲敾抐偡傞偙偲傕偱偒傑偡丅
掕悢崁偺専掕偵偮偄偰偼桳堄偱偼偁傝傑偣傫偑丄偙偺抣偼偨偩夞婣幃偺摉偰偼傔傪傛偔偡傞偨傔偺傕偺偱偡偐傜偁傑傝廳梫帇偡傞昁梫偼側偄偐偲巚傢傟傑偡丅
嘍曣夞婣幃傪悇掕丄梊應偡傞丅
愢柧曄悢乮倃1丄倃2丄丒丒丒倃倫乯偑擟堄偺抣乮倃10丄倃20丄丒丒丒倃倫0乯傪偲傞偲偒丄梊應抣Y0^偺梊應嬫娫乮怣棅棪兛乯偼師偺傛偆偵偟偰媮傑傝傑偡丅
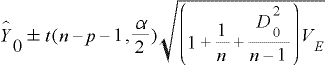
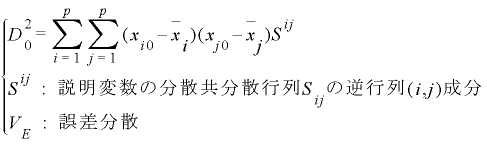
D0^2偼儅僴儔僲價僗偺斈嫍棧偲屇偽傟傞傕偺偱擟堄偺抣乮倃10丄倃20丄丒丒丒倃倫0乯偲乮倃1丄倃2丄丒丒丒倃倫乯偦傟偧傟偺暯嬒偲偺摑寁揑側嫍棧傪昞偟傑偡丅
椺偊偽杮椺偱乭倃侾亖俀乭丄乭倃俀亖侾乭偲偟偨応崌偺梊應嬫娫乮怣棅嬫娫俋俆亾乯偼師偺傛偆偵側傝傑偟偨丅

-------------------------------------------------------------------------------------------
埲忋嘆偐傜嘍傑偱偑廳夞婣暘愅偺偍偍傑偐側棳傟偵側傞偐偲巚偄傑偡偑丄嘍偺梊應偵娭偟偰偼憡応偺暘愅偵偼柍堄枴側偙偲偩偲峫偊偰偄傑偡偺偱丄幚嵺偺暘愅偼嘆偐傜嘋傑偱墴偝偊偰偍偔偖傜偄偱廫暘偱偡丅
杮椺偺応崌丄嶶晍恾偲廳憡娭學悢丄嘊丄嘋偺専掕偺寢壥偐傜愢柧曄悢乭倃1乭偺傒偺梫慺傪庢傝擖傟偰丄師偺傛偆側儖乕儖偺攧攦僔僗僥儉傪嵦梡偟傑偡丅
慜偺廡僒儎偑奼戝偵摦偄偨応崌偼弅彫偺僒儎庢傝億僕僔儑儞傪嶌傝丄廡枛偵庤巇晳偄偟傑偡
慜偺廡僒儎偑弅彫偵摦偄偨応崌偼奼戝偺僒儎庢傝億僕僔儑儞傪嶌傝丄廡枛偵庤巇晳偄偟傑偡
偙偺儖乕儖偱僔儏儈儗乕僔儑儞攧攦偟偨応崌埲壓偺傛偆側寢壥偲側傝傑偟偨丅
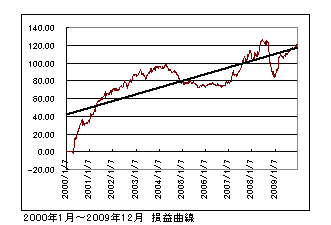 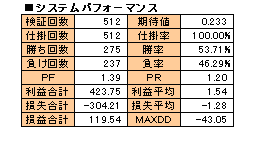
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俹俥 丗 僾儘僼傿僢僩僼傽僋僞乕
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俹俼 丗 儁僀僆僼儗僔僆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俵俙倃俢俢 丗 嵟戝僪儘乕僟僂儞
搑拞偵僔僗僥儉偑婡擻偟偰偄側偄帪婜傗戝偒偄僪儘乕僟僂儞傕傒傜傟傑偡偑寢壥偲偟偰侾俀侽pips晅嬤傑偱偒偰傑偡偺偱丄傑偢傑偢偺僷僼僅乕儅儞僗偱偁傞偲敾抐偱偒傑偡丅
偪側傒偵愢柧曄悢乭倃俀乭偺梫慺傪庢傝擖傟偰丄師偺儖乕儖傪晅偗壛偊偨応崌偺僔儏儈儗乕僔儑儞偼偙偆側傝傑偟偨丅
慜偺廡偺乭倃俀乭偺愨懳抣偑乭倃俀乭慡僨乕僞偺昗弨曃嵎傛傝戝偒偄応崌偼巇妡偗傪尒憲傞
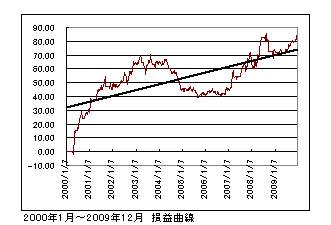 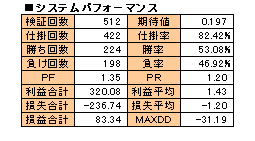
儖乕儖傪捛壛偟側偄応崌偲偝傎偳曄傢傝偼側偄姶偠偱偡偑丄侾夞偺攧攦偵偍偗傞懝塿婜懸抣偺僷僼僅乕儅儞僗偑棊偪偰偄傑偡丅傗偼傝乭倃俀乭偺梫慺傪庢傝擖傟偰偺捛壛儖乕儖偵偼偁傑傝岠壥偑側偄偲敾抐偟傑偟偨丅
仠偙偺復偱徯夘偟偨廳夞婣暘愅偺奺庬摑寁検偼師偺僄僋僙儖偺娭悢傪巊偭偰寁嶼偱偒傑偡丅
LINEST()娭悢傪巊偊偽丄夞婣學悢丄昗弨岆嵎丄廳憡娭學悢側偳昁梫側摑寁検傪偄偭偒偵媮傔傞偙偲偑偱偒傑偡丅INDEX()娭悢傗OFFSET()娭悢側偳傪慻傒崌傢偣傟偽昁梫側摑寁検傪岲偒側晽偵庢傝弌偡偙偲傕偱偒傑偡丅
乮椺乯 =INDEX(LINEST(OFFSET(A1,0,0,COUNT(A1:A100),1)
暘嶶偲嫟暘嶶偺抣丂=COVAR(攝楍 1,攝楍 2)
俥抣丂丂丂=FINV(桳堄悈弨兛,帺桼搙fR,帺桼搙fE)
倲抣丂 丂丂=TINV(桳堄悈弨,帺桼搙fE)
媡峴楍丂=MINVERSE(峴偲楍偑摨偠悢偺攝楍)
|

