|
サヤ取りを行う場合サヤの周期を確認して仕掛けるタイミングもしくは仕切るタイミングを計ることが重要です。一見して一方的に拡大したりまたは縮小したりするサヤでも、波を分解してみると細かい波の成分がたくさんあることわかります。これらの波の成分を解析的に算出する方法がフーリエ解析です。
フーリエ解析をする前にフーリエ級数についての理解が必要です。厳密的なことは割合しますがフーリエ級数とは与えられた周期関数は正弦(SIN)と余弦(COS)の合成で表すことができるというもので、サヤの変動が周期関数であるならサヤの動きはフーリエ級数式で近似されます。
周期=”2L”(波が1回上下する期間)を持つ関数のフーリエ級数式は(1)式で表されます。
(1)式のA0、An、Bnの項はフーリエ係数と呼ばれ、(2)式でそれぞれ表されます。
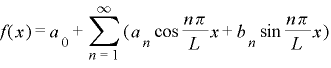 ・・・・・(1) ・・・・・(1)
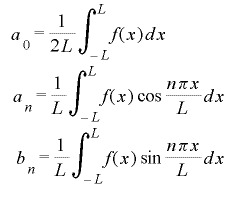 ・・・・・(2) ・・・・・(2)
やや繁雑な式に見えますが、An、Bnは振幅(波の上下する大きさ)、nπ/Lは角速度(単位時間あたりに進む角度)を持つCOS波とSIN波を1からnまで足し算したにすぎません。
さらにフーリエ級数式の周期”L”を-∞~∞まで全区間に広げて、(3)式のオイラーの公式(指数関数と三角関数が虚数を介して結びつく数式)用いて複素形式にて表すと、(4)式の複素フーリエ積分が導かれます。
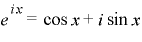 ・・・・・(3) ・・・・・(3)
”i”は虚数単位(i=√-1)を表す記号。”e”はネイピア数(e=2.7182・・・)
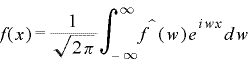 ・・・・・(4) ・・・・・(4)
ここでの”w”は周波数を意味します。
複素フーリエ積分(4)式の^f(w)の部分は(5)式で表されます。
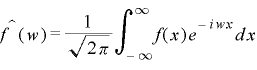 ・・・・・(5) ・・・・・(5)
^f(w)は周波数の関数を意味し、wとw+Δwの間の周波数にある振幅の強さを指し、スペクトル密度と呼ばれます。
また(5)式は関数f(x)を関数^f(w)に変換するフーリエ変換といい、工学の分野で境界値問題を含む微分方程式の解法などに応用されます。逆に関数^f(w)から関数f(x)に変換する操作をフーリエ逆変換といい、(4)式でフーリエ逆変換されます。
さてここから実際のサヤデータを用いてフーリエ解析を行ってみましょう。フーリエ解析をするにあたって上で説明したような積分の計算などわからなくても、エクセルのツールを使えば簡単に解析することが可能です。ただしここで説明されているフーリエ級数やフーリエ変換の意味がわからなければ、エクセルで出力された結果の数字を見ても、その数字の意味が理解できないかもしれません。
例としてオーストラリアドル(AUD/JPY)とニュージーランドドル(NZD/JPY)のサヤデータ(128日分)を使用して、フーリエ解析を行いサヤの周期を検証してみましょう。下のエクセルシートの図を見ながら解析の手順を踏みます。
図1 フーリエ解析エクセルシート
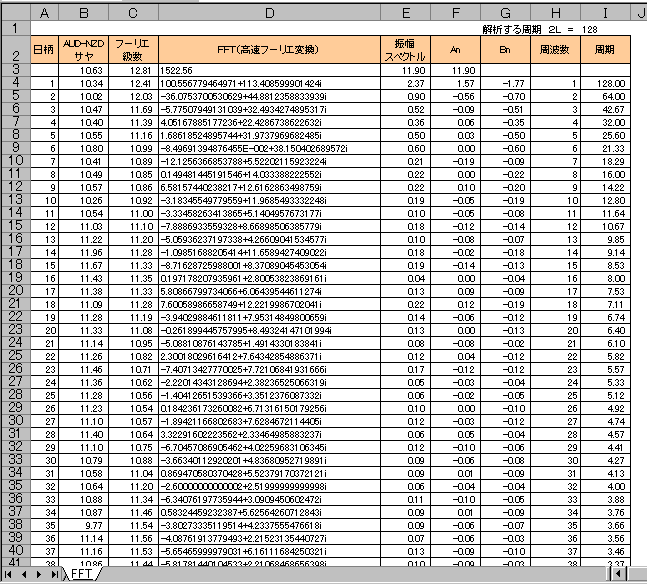
まず準備として図1のB列に解析するデータを入力します。(ここではAUD-NZDのサヤデータになります)
ここで注意することは、エクセルでのフーリエ変換は離散フーリエ変換を高速化した高速フーリエ変換(FFT)のアルゴリズムが組み込まれていますので、データの数は2のn乗でなければなりません。例では2の5乗の128個のデータを扱いました。従ってA列の日柄は最初の行を0として最終行を127まで入力しています。
次にエクセルのツールを使いフーリエ変換を行います。
メニューから ツール ⇒ 分析ツール ⇒ フーリエ解析 を選んで”OK”を押します。(分析ツールがない場合はアドインを選んでインストールして下さい)
フーリエ解析のフォームが現れますので、入力範囲に解析するデータの範囲($B$3:$B$130)、出力先に出力先の範囲($D$3:$D$130)をそれぞれ指定します。そして”OK"を押せば出力先に解析値が出力されます。
結果を見ると”A+iB”のような複素数の形で出力されます。これの実数部分がCOSのの振幅、虚数部分がSINの振幅の成分を意味します。実数部分の値は関数”IMREAL()”虚数部分の値は関数”IMAGINARY()”を使えばそれぞれ値を取り出すことができます。またそれぞれの値を解析する周期で割れば(2)式のフーリエ係数が求まります。
セル I1 ⇒ =COUNT(B:B) ”あらかじめ解析する元データの周期をこのセルに出力させておきます”
セル F3 ⇒ =IMREAL(D4)/$I$1 ”フーリエ係数A0を計算します。周期2Lで除算します”
セル F4 ⇒ =IMREAL(D4)/($I$1/2) ”フーリエ係数Anの項を計算します。周期Lで除算します”
セル G4 ⇒ -IMAGINARY(D4)/($I$1/2)
”フーリエ係数Anの項を計算します。周期Lで除算します。SIN部分は符号が逆転します”
セル F4、G4をコピーしてその列の最終行まで貼り付けすると各周波数に対するフーリエ係数が求まります。
次にフーリエ係数Anを横軸にBnを縦軸に取ってベクトルの合成値を計算します。これが振幅スペクトルになります。
セル E3 ⇒ =SQRT(F3^2+G3^2)
”合成値(スペクトル)はピタゴラスの定理より算出されます。同様にコピーして下行に貼り付けます”
周波数は”セルH4”を1としてから下行に127まで入力します。
それぞれの周波数に対応する周期は
セルI4 ⇒ =$I$1/A4 と入力してそれをコピーして下行に貼り付けます。
ここで各周波数に対するスペクトルを棒グラフで表してみましょう
図2 振幅スペクトル

解析データ数の半分までスペクトルを計算することができます。残りの半分は鏡像となって同じ数値に出力されますので無視して結構です。グラフ見ると周波数1から6の辺りまで強いスペクトルあるのがわかります。
そこでスペクトルの強度の順番に解析データを抽出してみます。
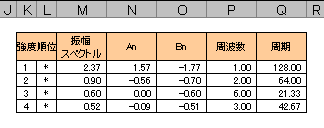
再び図1の下の方の表(同じエクセルシートになってます)をみて見ましょう。1番から4番目までの強度順にデータを抽出しています。K列に強度の順位を入力して、L列に”*”アスタリスクなどフラグを入力します。
セル M3 ⇒ =IF(L3="",0,LARGE($E$4:$E$66,K3)) ”K列で入力した順位の振幅スペクトルを出力します”
セル N3 ⇒ =IF(L3="",0,VLOOKUP(M3,$E$4:$I$66,2,0)) ”同様にフーリエ係数Anを出力します”
セル O3 ⇒ =IF(L3="",0,VLOOKUP(M3,$E$4:$I$66,3,0)) ”同様にフーリエ係数Bnを出力します”
セル P3 ⇒ =IF(L3="",0,VLOOKUP(M3,$E$4:$I$66,4,0)) ”同様に周波数を出力します”
セル Q3 ⇒ =IF(L3="",0,VLOOKUP(M3,$E$4:$I$66,5,0)) ”同様に周期を出力します”
セル M3、N3、O3、P3、Q3をコピーして下行に貼り付けます。
この結果から以下の4つの強いサヤの周期の成分があることが判明されました。
強度順位1 周波数1 周期128日
強度順位2 周波数2 周期64日
強度順位3 周波数6 周期21日
強度順位4 周波数3 周期42日
この内周波数1は解析期間の周期であるため、分析結果からは外さなければなりません。
よってサヤ取りを仕掛ける場合、この解析結果から長期的には周期64日の半分である32日を目安に、中期的には42日半分である21日を目安に、短期的には21日の半分である10日を目安にトレードを行えば行えば良いといえます。
次に求めた上位4つの強度を持つ波形を波1~波4として、それぞれの波形を視覚的に確認するために、フーリエ級数式で表してみましょう。
例えば波1ですが、Xを日柄として、A0はセル”F3”の値、An、Bnをそれぞれ(1)式に代入して波1の式を作ります。
=$F$3+$N$3*COS(2*PI()/$I$1*$P$3*A3)+$O$3*SIN(2*PI()/$I$1*$P$3*A3) ”波1式”
を入力して下にコピーすると波形が完成します。同様に波2から波4も波形を作成しグラフにプロットしたものが図3です。
=$F$3+$N$4*COS(2*PI()/$I$1*$P$4*A3)+$O$4*SIN(2*PI()/$I$1*$P$4*A3) ”波2式”
=$F$3+$N$5*COS(2*PI()/$I$1*$P$5*A3)+$O$5*SIN(2*PI()/$I$1*$P$5*A3) ”波3式”
=$F$3+$N$6*COS(2*PI()/$I$1*$P$6*A3)+$O$6*SIN(2*PI()/$I$1*$P$6*A3) ”波4式”
図3 強度上位4位の波の波形
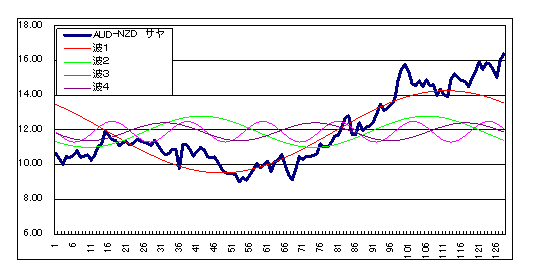
求めた波1~波4を合成してフーリエ級数式をプロットすれば図4のように実際のサヤの変動に良く当てはまります。
セル C3に以下の波1から波4を合成したフーリエ級数式を入力して下のセルへコピーすれば完成です。
=$F$3+$N$3*COS(2*PI()/$I$1*$P$3*A3)+$O$3*SIN(2*PI()/$I$1*$P$3*A3)
+$N$4*COS(2*PI()/$I$1*$P$4*A3)+$O$4*SIN(2*PI()/$I$1*$P$4*A3)
+$N$5*COS(2*PI()/$I$1*$P$5*A3)+$O$5*SIN(2*PI()/$I$1*$P$5*A3)
+$N$6*COS(2*PI()/$I$1*$P$6*A3)+$O$6*SIN(2*PI()/$I$1*$P$6*A3)
図4 波の合成(フーリエ級数)
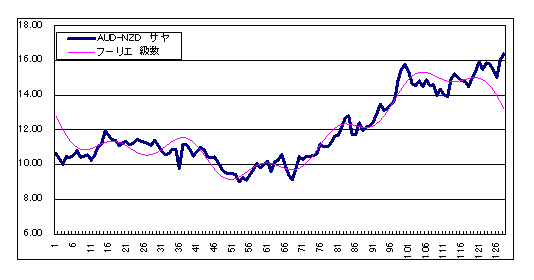
またセル L3からL6までフラグとして”*”を入力していましたが、これを削除すれば、この周波数の成分の波形を消すことができます。また図3のような1つの波だけ表示したり、いろいろな周波数の波形を組み合わせて作ったりすることもできます。
実測値に曲線が当てはまっていると見栄えもよくかっこいいのですが、ここでの解析は予測式を作って変動を予測しようというものではなく、あくまでのサヤの変動周期の成分を解析して建玉どこまで維持するかの目安を作るのが目的です。あたりまえですが、フーリエ級数式は解析期間の相場の動きにはとてもよく当てはまりますが、それ以外ではほとんど当てはまりません。
|

